2020/7/1
　そもそもA・AB・B級動作とはアイドリング電流や動作時の電流変化により分けられます。C級動作なんて動作条件もありますが、C級動作は高周波の世界の話でありオーディオアンプでは使いません。

　近年では何故かD級アンプなんて物もあります。あれは私の思いますに恐らくデジタルアンプの事を意味しているのでは ?　しかし、そもそもデジタルアンプなど世の中にありません。現在デジタルアンプと呼ばれている物はPWMコントロールと云う物で決してデジタルなどではありません。PWM動作とは近年のエアコンのコントロール回路です。そのコントロール周波数を人の可聴域の上の周波数でコントロールしているのです。要するにデジタルデーター回路などではありません。

　そこでこのページではその話しは先送りと云う事で先ずは古典的回路からお話を進める事に致します。

　最も古典的回路はトランス結合回路だと思います。これには色々な意味合いがあります。先ずは当時の真空管は増幅率が足りずにトランスの巻き線数で増幅率を稼いだ事が挙げられます。更に当時のパワー管はグリッドの整流電流が多く流れ、その整流電流をトランスで吸収してしまおうとしたアンプです。しかし、何故か未だにトランス結合回路に拘ったお方も居られるようです。その代表的存在が房総半島のとっつぉきでレストランを営んでおられお方なのですが、現在は私はその後の事は知りません。

　私も昔々のトランス結合アンプに凝った時期がありました。しかし、トランス結合アンプは出来上がりが予測出来ません。更に音質についても予測不能なのです。そこでほんの僅かの期間で止めてしまいました。

　当時の製作記事を観て見ますと何故か巻き線数とインピーダンスに勘違いをしている記事があります。例えば　10kΩ::40kΩ　のインターステージトランスがあったとします。その場合のトランスの実際の巻き線数は二次側は平方根に比例します。するとこのトランスの場合の増幅率は二倍となります。

　このドライブ電圧にも妙な物があります。例えば UV-845　です。UV-845はフ゜レートの供給電圧1000Vの時のバイアス電圧は170Vです。するとドライブ電圧として約70パーセントの119Vが必要です。しかし、そのアンプのドライバー管は何故か6SL7なんです。更にプレートの供給電圧は僅か350Vなんです。全く足りません。そんなパワーアンプが平気で売られているのです。

　確かに何も知らないオーディオマニアも悪いと思いますが、そのようなパワーアンプを平気で売っているガレージメーカーはもっと悪いと思います。

　長くなりましので次回に続きます。次回はRC結合のシングルアンプについてにしましょう。

2020/6/19
　私は何を考えていたのでしょう ?　何とパワーアンプ事をすっかり忘れておりました。少々、多少、大分ボケが進みましたかね　!

　スピーカーに関してはパワーアンプについての後にしましょうね。

　パワーアンプについてもこれまた大変な内容になります。何せパワーアンプの場合はその他機器よりももっともっと幅広く散在する内容が存在します。何せ遠い々昔々の物が現存している場合もあれば、当時のデイバイスである昔々の真空管があれば当時の内容でそのまま現在に蘇らせる事も可能です。要するに暦を約ではありますが100年程度戻す事が可能なんです。要するに当時のオージオンも手に入れば当時のアンプも再現可能と云う事になります。

　しかし、ここでそのような事を論じても面白くも楽しくもありません。そこで可能な限り現実的なお話に限定する事に致します。すると話はかなり狭まります。真空管に関してはせいぜい　45(245)　から程度になりますかね。或いは　10　程度まで遡っても良いかも知れません。何せ未だに昔々の真空管にある意味憧れを抱いているお方が多いと云う事は免れませんのでね。

　しかし、世の中はやはり現実的なお話が善いのでは ?　とは申せその手のお方達は自分が好み、没頭している世界が当人にとっては当たり前であり他の方達が変なのであります。これは正に宗教の世界に近いお話になってしまいます。と、言う私もかつては非常に偏った世界に没頭していた経験がありあまり偉そうな事は言えません。

　しかし、私の場合は幸いにもその世界から抜け出す事が出来ました。結果としてそれらの経験が出来ましたので　「良かった、良かった」　なのであります。

　さてさて、パワーアンプは大別して真空管式とソリッドステート式に分けるのが普通の分け方だと思います。その中でソリッドステート式は回路方式も現在ではほぼ固まっています。それは差動回路入力によるSEPP(シングル　エンデッド　プッシュ　プル)出力回路です。その中で昔流行ったA級動作パワーアンプも既に廃れて現在ではほとんどの物がAB級によるパワー回路となっているようです。

　このA級やAB級、B級に関しては真空管式に於いては未だ意見が分かれているようです。中にはB級アンプとはB級グルメと同じように考えているお方もいるようで、要するに一級品では無いアンプだと勘違いしているお方も居られるようで笑える話です。

　そもそもB級グルメなんて言葉を使ったのが間違えで例えばご当地グルメとかオリジナルグルメとか、その他それらしい呼び方をすべきだと思っております。

　さてさて、そこでここでは真空管式に的を絞って話を進めたいと考えております。しかし、それでも真空管式パワーアンプに関しては多岐に渡ります。中には面白いお話や笑いたくても笑えない話までに至ると思います。

　長くなりましたので次回に続きます。

　ベーリンガーのECM8000は測定用の物でデーターとしては20～20kHzとなっております。勿論コンデンサー型です。しかし、これは残念ながら私の所では確認の方法がありません。　このマイクは時として我が町会の祭りの時にPA用に使っておりす。その場合の音としては何せ装置が装置ですので音質云々のレベルではありませんので割愛致します。

　私は以前ソフトの録音の場に居た事があります。その時に感じた事は録音の場で清々しい音の録音はノイマンの87が優秀なようです。或いはAKGの414が優秀だと思います。近年はマスコミの映像を見ているとB&Kの物が多用されているようです。

　いずれにせよソフトの音質が出音に大いに影響を与えますので装置の音質を確認する為には自分の好みの音が録音されているソフトで確認しませんと基本がズレてしまいます。更に録音方法にも大変に影響されます。例えばデッカ・ロンドンの録音は実際には我々がコンサートで聞いても聞けない音で録音されていますので比較対象とするには問題ありの音だと思います。

　しかし、このように申しましても余りにも混沌としたお話にしかなりません。要するにそこに答えなどないのです。そこで私は自分で許せる音を発するすスピーカーを選択するのが唯一絶対の方法だと思っております。問題はその時に自分が許せる音をいかに選択するか ?　なのです。

　私としてはこの選択の時にフルレンジ型としては昔々のマグナボックスの励磁型が一つの答えとしたのです。更に・・・。

　次回に続きます。

2020/5/28
　いよいよスピーカーについての項なのですが、これがまたまたスピーカーには余りにも問題が多過ぎてどの問題をどのように説明したら良いのか ?　これまた難しい問題なのです。これらの問題の中で最も大きな問題が皆様の音の好みの問題なのです。中には低音らしきボンボンと響き渡る音を好むお方も居られます。しかし、これはそのお方の好みですのでとやかく言う必要はありませんし、言ってはいけない事ですのでね。そこで先ずは私の好みの音と私自身が理想的な音とする音からご説明しようかと思います。

　私の好みの音を一言で説明しますと清々しいです。しかし、これが大変に難しい事であるし、またそのような清々しい音が録音されているソフトも限られた物しか無い事も原因しています。

2020/5/25
　久々の更新です。理由は　「オジンのたわごと」　にも書きましたがコロナ騒動で部品が手に入らずやる気が削がれてしまうっているのです。やはり私のように物を作る事に生きがいを感じてる者にとっては致命傷的出来事なんです。やはりにっくきは大陸の某国なんです。

　さてさて、トーンコントローラーの存在価値についてです。

　多くのオーディオマニアはトーンコントローラーは自らのシステムの音質を調整する物だと思っているでしょうね。勿論その目的もあります。理由は世の中のほとんどのスピーカーシステムは皆様が思っているほど高性能な物では無いのです。その証拠に近年のトールボーイ型スピーカーシステムの発する音はどれもこれも変な音を発する物ばかりです。要するに低音らしくボンボンと鳴り響くいまいましいくどい音です。あんな音を出す楽器は世の中にありません。楽器の発する音はほとんどの物が軽快で爽やかな音です。あんな耳障りな音の楽器など世の中にありません。

　その傾向は必ずしも小型のトールボーイ型スピーカーシステムに限りません。かなり大型のスピーカーシステムも近年の物はいまいましい音を発する物が非常に多いのです。

　しかし、これらは余りに宴色され過ぎておりますので直しようがありません。まともな物に買い換えるしか方法はありません。しかし、そればかりではありません。ソフトにも大いに問題有りなのです。近年の若者向けソフトには凄まじい物があります。何せ私の装置で聞いておりますと時としてウーハーが底を打ってしまうソフトがあります。では、原因は ?

　その原因はソフトの最終段階のトラックダウンの時に小型のラジカセで音を調整しているからなんです。要はラジカセでは聞き分けられない超々低音が入っている事がエンジニアーには解らないのです。するとそのまま最終盤としてソフトを作ってしまうのです。

　私は勿論そのようなソフトを聴いている訳ではありません。それらは私が仕事中に絶えず流しているコミュニティーFM放送に時として流しているのです。これらはFM放送局でも解りません。何故ならFM放送局のモニタースピーカーもそこまでの性能を持ち合わせていないからです。それではどうしたら良いのか ?

　次回に続きます。

　クリスタル型カートリッジとは素材はロッシェル塩です。外部から力を加え変形させると電圧を発生します。しかし、ロッシェル塩は湿気に弱い事もありその後はセラミック型へと進化して行きます。その最終的な姿は現在のガスコンロの点火装置とかガイライターの点火装置となって現在に残っております。工業用の大型ガスバーナーの点火装置なども同じです。

　ここで少々面白い話をしましょう。それはガスバーナーの点火装置の話しです。この話はオーディオにも及びますのであえてお話する事にします。

　某工場でガスバーナーの点火装置が故障しました。そこで素人が改造して点火装置のリード線に高圧線ではありますが一般用の物を使ったのです。しかし　「音はすれども火が付かず」　だったのです。その使った電線はクロムメッキかニッケルメッキが施されていました。

　電気は、特にパルスの場合は電線の表面を流れます。すると銅よりもクロムやニッケルの場合は抵抗値が高いのです。するとパルスがパルスでは無くなってしまうのです。その結果発電素子であるロッシェル塩やセラミックの鋭いパルスが潰れてしまいスパークしなくなってしまったのです。

　電線には色々な種類がありますが点火用の電線は高圧線ではありますがメッキ線は使いません。一般用の電線を使う場合には昔の四種線が良いのかも知れません。四種線など言っても知らない人がほとんどでしょうね。

　我が家は古い家ですので天井裏の配線は四種線です。四種線のノップ碍子配線です。よって、漏電はありません。ひょっとしてスピーカーケーブルには静電気の発生は無い四種線が良いのかも知れません。但し、現在は四種線は世の中にありませんので残念ではあります。

　今回も少々変な話しになりました。次回はトーンコンローラーの存在価値についてです。

　写真の物がそれです。要するに一体型のステレオ装置と言った方が解り易いと思います。我が家にもありました。

　これで優秀な音が再生されるとは思いませんよね。しかし、当時はそれでも満足して聴いていたのです。しかし、海外では当時からシーメンスのオイロダインとかジムラン(JBL)ハーツフィールドとかアルテックにはその後のA5・A7の元になる物がありました。

　当時は1ドル360円の時代です。庶民にはとてもとても買える物ではありませんでした。またそのような物を買おうとする気持ちも趣味も無い人がほとんどだったと思います。更にオーディオ機器に関しては1ドル千円程度に値したと思います。当然気が遠くなるような世界だったのです。

　これらのステレオに使われていたレコード再生用のカートリッジはほとんど全てクリスタル型と言われた物でした。

2020/3/10
　トーンコントロールなんて聞くと　「そんな物 !」　と思う人は多いと思います。しかし、そのような人の多くが実際には使った事が無い人がほとんどだと思います。何せ近年のプリアンプの多くの物が装備しておりませんのでね。その理由は後述と云う事で。

　先ず皆様に問いたい事は　「そんなに立派なスピーカーシステムをお使いですか ?」　なんです。そもそも現在の数十万円から数百万円の物はほとんどの物が単に値段だけのまやかし物と言って間違い無いと思います。要するに高いお金を払った事に満足していると云う事です。これは例えば受験生が高い参考書を買ってそれで満足してしまい実際の勉強はやっていないのと同じです。要するに

　左の写真は何回も示している私が産まれた頃のマグナボックスの30cmフルレンジスピーカーです。非常に軽快で素直な音のユニットです。このようなスピーカーですと充分な効果を示すであろうと思います。要するに薄化粧の日本美人的な音質で音楽を楽しく聴けるようになると思って下さい。

　しかし、現在の多くのスピーカーシステムはあまりにも演出されており、更に化粧を施しますとしつこくなってしまうのです。しかし、もう少し穿って考えてみましょう。要は　「ソフト側の音質は ?」　なんです。

　昔の録音は録音装置が幼稚でしたのであまり加工されておりません。すると聞く側で調整してもそれ程変な音にはなりません。それどころか方法によっては非常に聞き易く楽しく聴く事が出来る場合が多々あります。しかし、現在の録音は何でも有りです。すると　「過ぎたるは尚及ばざるが如し」　になってしまうのです。

　これ以上申し上げますと　「オジンのたわごと」　になってしまいますのでこれ以上は何も申しません。

　このような事もありアマチュアの間では普及しなかったと思っております。しかし、実際に使ってみると便利なコントローラーだったと思い出します。理由は当時のスピーカーシステムの性能は誉められた物ではありませんでした。それをごまかしてくれたコントローラーだったのだと思います。しかし、いずれにせよ私が小学生の頃の思い出ですのでこの意見は定かではありません。

　更に当時の我が家のオーディオ装置はモジュラー型と呼ばれた貧弱な物でしたので子供の私には便利な物だと感じたのかも知れません。

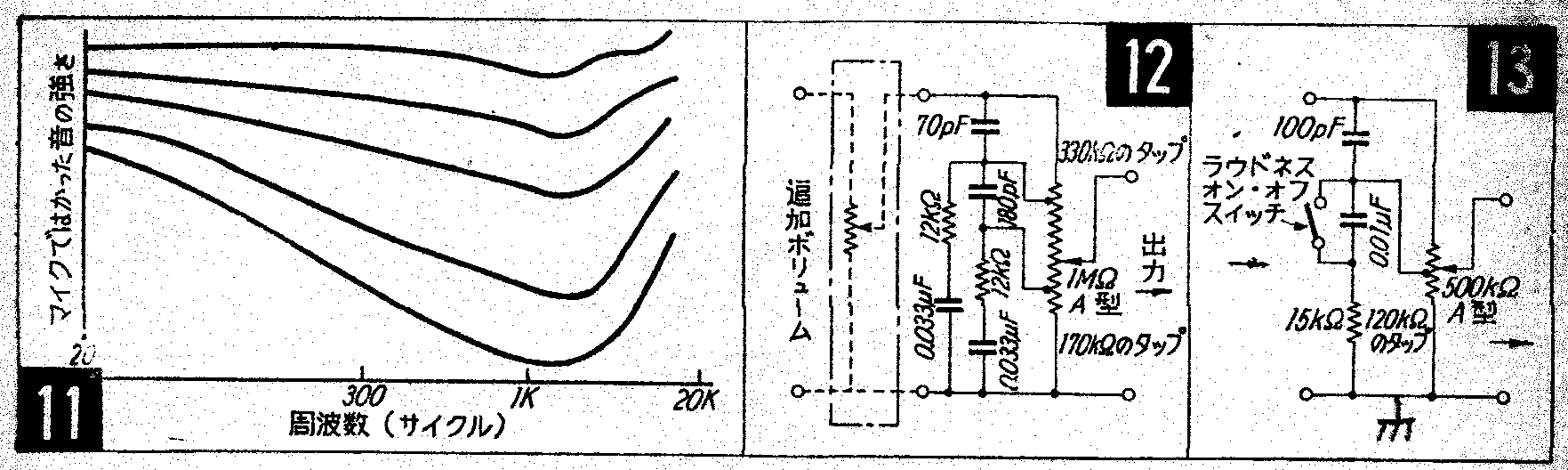
　仮に中点付きのボリュームが手に入るのであれば　13　の回路は有効に使えると思います。しかし、安易に作りますと失敗します。それは回路定数を観てもらえれば解ります。先ずは入力インピーダンスは低いので前段の出力インピーダンスは低い事が要求されます。更に出力は500kΩのボリュームが付されております。するとこの出力を受ける回路の入力インピーダンスは充分に高い事が要求されます。これらの条件を満たすにはリニアーICを使うしか無いと思います。すると当時の真空管式回路では無理だったのです。よって、当時でもラウドネスコーントローラーを入れると音質劣化になるのであまり普及はしなかったのだと思われます。

　更に現在に至っては大きな問題があります。それは現在の異常に演出された音作りのスピーカーシステムでは演出し過ぎになってしまう事です。これはいずれスピーカーシステムの問題についての項で説明すると思いますが、要するにレディー・ガガのようになってしまうのです。意味は解ると思いますので詳しくは説明しません。

2020/4/6
　プリアンプのコントローラーについてです。

　オーディオ黎明期には色々な効果を示すコントロール回路が装備されておりました。それらはラウドネスコントローラー・ランブルフィルター・ハイカットフィルター(スクラッチフィルター)・トーンコントローラー・L・Rバランスコントローラーなどなどです。

　これらの中で現在に至ってはランブルフィルター・ハイカットフィルー(スクラッチフィルター)は不要であると以前申し上げたと思います。ではその他の付属回路は ?

　私はトーンコントローラーは必要であると考えております。その他の回路に至っては可能であれば　L・Rバランスコントローラー程度だと思っております。それでは可能な限りご説明しましょう。先ずは現在ではほとんど忘れ去られたラウドネスコントローラーからです。

　ラウドネスコントローラーとは基本的に我々の耳の特性が元々持っている特性を自動的に調整しようとする積極的なコントローラーです。回路は下に示します。

2020/3/24　　　　ちょっと一服
　このページはオーディオのページにも関わらず音の話はほとんど出て来ません。本日はちょっと一服してその理由について少々。

　更に理屈と理論の積み重ねで皆様うんざりしてしまうでしょうね。そんな事より

　　　　　「早く音の話しにしてくれ !」

　だと思います。しかし、しかしなんです。オーディオとは電子回路の積み重ねであり、更に非常なる厄介者のスピーカーが最終負荷です。そこにはやはり理論の積み重ねが必要なんです。その集大成が最終的な音なんです。よって

　　　　　「理論の積み重ね無くして良い音は無し」

　なんです。

　理論を無視して単に感覚で組み上げた装置が

　　　　　「そんな筈では無かった !」

　なんて事になってしまうのです。例えばかつての名機の真空管式プリアンプに最新のトランジスター式ハイパワーアンプで組み上げたとします。しかし、出て来た音はけじめの効かないフニァフニァな音だったなんて事は当たり前に起こります。このページを真面目に理解しながらお読みになったお方なら原因は解ると思います。そうです、インピーダンスのミスマッチが原因です。

　多くのお方はプリアンプはプリアンプであり、パワーアンプはパワーアンプであり別物とお考えだと思います。しかし、電子回路としては両者一体として考えなくてはならないのです。

　更に真空管式A1級のシングルアンプがお好きなお方が近年の超低能率電気コンロ型トールボーイスピーカーシステムを鳴らしたならば正にフニァフニァな音でしか鳴ってくれません。理由はパワーアンプのダンピングファクターと出力にあります。要するに組み合わせは非常に大切な選択の要素となるのです。

　最終的な音質とはこれらを考慮した結果の音としての推測された結果としての音であるべきなのです。その為にはやはりそれなりの理論が理解されていませんと良い結果は得られません。最終的な音質に関しては、それらが成し遂げられた上に成り立つ好みの世界となります。

　今回は　「ちょっと一服」　の積りがやはり少々理屈っぽい話し」　になりました。失礼しました !

　次回はプリアンプの音質コントロール回路についてです。

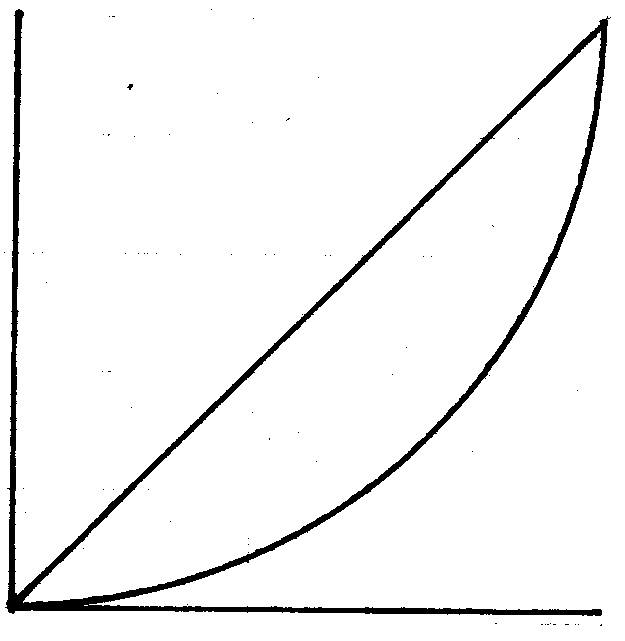
　では、何故オーディオ機器の場合はA特性の物を使うのか ?　なんです。その理由は最初は徐々に音が大きくなり、ある程度回した位置になりますといきなり音が大きくなる事に人は自然な動作と感じるそうなんです。しかし、一般家庭で数十ワット、数百ワットなんてパワーアンプを使いますと回し始めの位置でも必要以上な音圧になってしまいます。それを防ぐにはやはりプリアンプにはゲインコントローラーを入れるべきだと私は思います。

　しかし、各アンプメーカーはそれをやろうとしません。原因はオーディオ機器メーカーの技術やは元々オーディオマニアではないからだと思っております。要するに各オーディオ機器メーカーは使う側の事など考えていないのだと思います。私に言わせればメーカー失格です。

　　

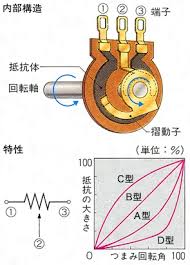
　構造としては図のようになります。ここで問題なのは果たしてカーボンの被服は正確な値で推移しているのか　?　なんです。例えばB特性の場合は均一な被服です。するとほぼ正確な値で推移する物が製作可能だと思います。問題はオーディオ機器で多く使われるA特性のものです。私は正確に推移する被服を塗布するのは非常に厄介な事だと思います。それが為にボリュームを絞って行きますと片チャンネルの音が無くなってしまうなんて現象が起こるのです。

　勿論この現象は使う側の無知に起因している事は言うまでもありません。私はボリュームの使い方はその装置の効率、その他の条件に則した物にすべきと思っております。そこでまたまたオーディオマニアはオーバースペックがお好きとなるのです。何も一般家庭で音楽を聞くのに数十ワットも、増してや数百ワットものパワーは全く不要な物なのです。

　私はやはりニーズに則した機器を使うべきだと思っております。

　このゲインコントローラーは私が自家用として何年も前から使っておりました。その調整範囲は　-30～+20dB　に達します。するとほとんどの場合に適合する結果となりました。

　更にプリアンプのボリュームを相当に上げた状態で音楽を楽しむ事が可能になりました。やはりボリュームはなるべく上げた状態で使う者だと実感したものでした。

　そこでやはり一般のプリアンプの場合でもゲインコントローラーは入れるべきだと思っております。

　するとオーディオ機器に使われているA特性のボリュームは果たして正しいのか ?　になります。

　次回はA特性ボリュームとB特性ボリュームについてです。

2020/3/22
　今回のお話は広大な条件の下存在するオーディオ機器に対する対処方法についてです。

　例えば2A3によるロフチンホワイトアンプの場合は約0.3Vで最大出力に達しました。この場合について考えてみましょう。

　2A3のロフチンホワイトアンプの最大出力は昔の真面目に作られた2A3であれば最大出力は約3ワットです。しかし、現在の2A3の多くは1.5～2ワット程度しか出ないようです。これには少々がっかりですが、それでも昔の能率の良いスピーカーであれば10畳程度の部屋であれば充分な音圧で楽しく音楽が聞けたものでした。この場合の動作条件を考えてみましょう。

　カートリッジの出力電圧が3mVだったとします。その出力電圧を普通のフォノイコライザーであれば40dB(100倍)に増幅します。するとそのフォノイコライザーの出力電圧は300mV(0.3V)です。するとこの場合でも増幅率1の0dBフラットアンプで充分な事になります。しかし、オーディオマニアは何故か　「大きい事は良い事だ」　で例えばKT88のプッシュプルアンプやそれらに順じたパワーアンプを好んで使っていたものでした。この場合を考えてみましょう。

　当時の真空管式のパワーアンプの多くの物が1～2V程度で最大出力に達しておりました。この場合にKT88のプッシュプルアンプの最大出力は真面目に作ったものであれば数十ワットありました。これが私の言うオーバースペック以外の何物でも無いのです。

　現在でもこのような使い方で動作させている装置はいっぱいあると思います。更に多くのプリアンプに内蔵されたフラットアンプは十数dBの増幅率を持った物がほとんどです。するとどんな事が起こるか ?

　プリアンプのボリュームが上げられないのです。更に深夜になりますと更にボリュームを絞って使います。するとどんな事が起こるか ?

　ボリュームはオーディオ用の物は少々いい加減な物がほとんどなんです。するとボリュームは回し始めと回し終わりの部分の誤差が大きいのです。その結果片チャンネルの音が無くなってしまったなんて事が当たり前に起こりました。これは現在でも当然続いていると思います。

　この場合の対処方法はフラットアンプにゲイン調整回路を設けるしか他に方法はありません。更にボリュームは何故かフル状態の時の方が音質が良いのです。要するに多くのオーディオ装置は最悪の状態で使っている事になるのです。

　これは当方の手前味噌になりますが私が開発したゲインコントローラーは大変に有効なんです。

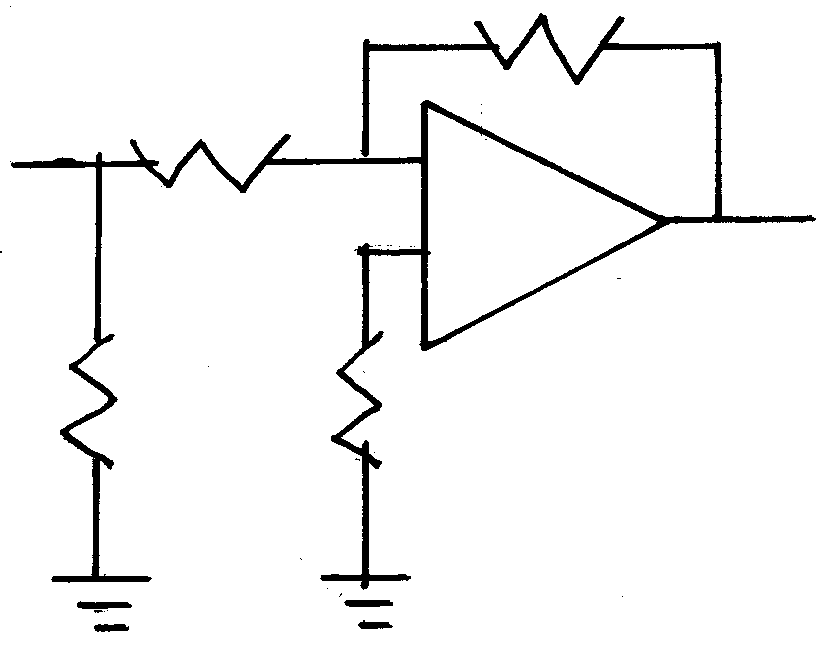
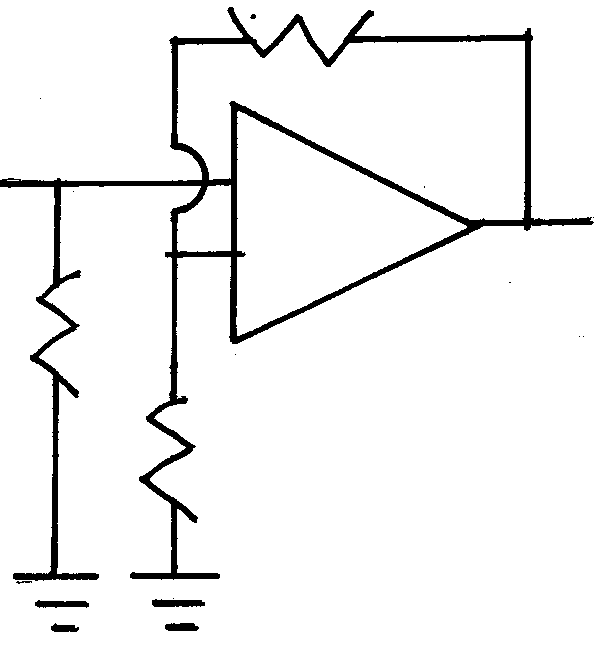
　逆相増幅回路の場合は　-端子　に入力します。+端子　は直接接地しても良いのですがもしもの為に数キロΩから数十キロΩで接地した方が安心です。この場合に　+端子　はゼロ電位です。当然接地電圧もゼロです。この状態をイマジナリーアースと言います。

　この回路の場合の増幅率は

　　A=R6/R5

　です。すると例えば　R6　を短絡しますと

　　A=0/R5

　となり、増幅はせずに出力は　ゼロ　となります。要するに　NF型ボリューム回路　となるのです。

　以上、この逆相増幅回路を二段重ねますとゲイン調整回路付きフラットアンプの出来上がりとなります。

　次回はゲイン調整回路付きプリアンプの存在意味についてです。

2020/3/12
　　ここで逆相について少々。逆相とは読んで字の如しで位相が逆になる増幅回路です。

　何故かアナログ屋さんは位相と云う言葉が好きです。それに対してデジタル屋さんはビットと云う言葉が好きです。アナログ屋さんは何でもかんでも位相と云う言い回しで済ませてしまいます。しかし、位相には電流位相と電圧位相の二種類があります。果たして皆様はどちらを言っているのか ?　私には解りません。

　デジタル屋さんは何故かビットで何でもかんでも済ませてしまいます。例えば現在のCDは16ビットマシンが主流です。16ビットマシンとは16個の大きさの違う積木を自在に組み替えてアナログ量に変換するマシンです。では、ワンビットマシンは ?　これは解らない人も多いと思います。

　いやいや、例によって道草でした。

　多くのお方が逆相にすると音にならない何て考えているようです。しかし、例えば一個のスピーカーを鳴らしているのであれば全体の位相が逆になりますので音としては何ら変わる事はありません。それは例えば　JBL のスピーカーは昔は一般とは逆の位相動作をさせていました。恐らく昔の　D130　などは逆相スピーカーだと思います。これを確認するには乾電池を使いコーン紙が引っ込んだら逆相動作の物です。この方法はフルレンジユニット・ウーハー・ミッドバスユニットに限られますのでご注意下さい。

　更にもう一つ言わせてもらいますと昔のクォードのプリアンプです。フェノ回路は6267による一段増幅回路でした。一段増幅ですので当然出力は逆相です。しかし、それに対してオーディオ評論家もオーディオマニアも何も言いませんでした。恐らく位相の事が解っていなかったのだと思います。要するにレコードとFM放送は逆の位相で聞いていた事になります。しかし、現実としては何も問題は無いのです。

　要するに全帯域が同じ位相であれば何ら問題は無いと云う事です。

　さてさて。逆相増幅回路を図に示します。

　真空管式の場合はプリアンプに二台のパワーアンプを繋いだら音は半分になってしまった何て事は当たり前に起こりました。この原因は真空管式の場合は出力インピーダンスが高い為二台並列の負荷に対応出来なかった事が原因なんです。しかし、上記のバッファーを入れますと数台のパワーアンプを並列に繋いでも全く問題なく正確に音声信号を送り出します。出力インピーダンスとは事ほど作用に大切な事項なんです。

　多くのお方は　「機械は目に見えるから簡単だ。電気は目に見えないから難しい」　と言います。しかし、全て理屈で考えますと理解も出来ますし、更に問題点も解決可能なんです。

　次回は逆相増幅回路についてです。

　

　R1 は前段の負荷抵抗となり、更に　Q　のイマジナリーアースの両者の役割を果たします。

　この場合の　Q　の増幅率は

　　(R2+R3)/R2=A

　となります。例えば　R3　を短絡したとします。すると

　　(R2+0)/R2=A

　となり　Q　の増幅率は　R2/R2=1　となり増幅はしません。よって、正相増幅回路の場合は増幅率は　1　以下にはなりません。この回路は別名バッファーとも言います。バッファーとは緩衝回路であり無意味のように見えます。しかし、実際には大変な効果を示す回路なのです。それは出力インピーダンスを低くする事なのです。

　出力インピーダンスを極力低くしますと例えどのような負荷にも対応可能となります。これは近年のリニアーICの場合はほとんどの物が約400Ωまで対応するようです。すると600Ωのライントランスにも信号を送れます。更に一般的にはプリアンプに何台ものパワーアンプ、或いはその他の機器を接続する事が可能になります。

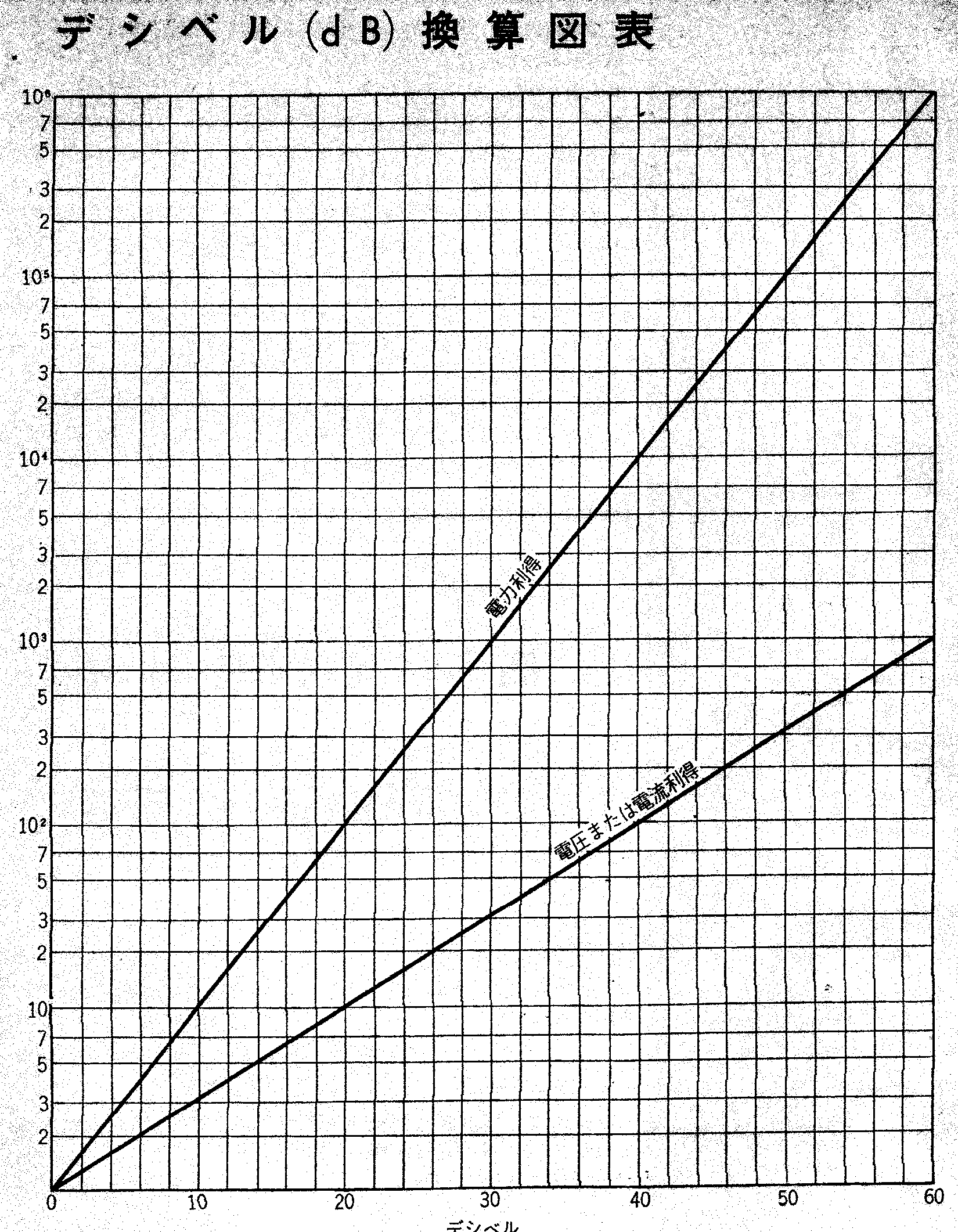
　このグラフは決して難しいものではありません。縦軸に対数を置いた片対数グラフです。横軸は当然普通のグラフです。

　この線を描くには縦軸の10の二乗点と横軸の40点と左の基点を結べば出来上がりです。読みは確かに正確無比と云う訳には行きませんがオーディオの場合ですとこれで充分役に立ちます。

　このグラフには電力換算表もあります。理由はベル博士は電圧・電流に関しては特例として　d　は1/20としましたが電力の場合は使い勝手に問題はありませんので　d　はそのまま1/10としたのです。そこでグラフには電力換算の線も引かれているのです。

　これで　dB　の意味がご理解頂けたと思います。しかし、ここでまたまた問題です。それは何故このような面倒な計算式を使わねばならないのか ?　です。

　その理由は弱電回路の場合加減乗除が自由に出来ます。しかし、実際にはほとんどのオーディオ回路は単に掛け算しか行っておりません。その典型的回路が一般に言うフラットアンプ回路です。

　しかし、実際には入力のボリュームで音声信号を分圧してレベルを下げて、更にフラットアンプで掛け算をして増幅しているのです。実にバカバカしい事を行っているのです。

　この場合に割り算を行ったり引き算を行えばこのバカバカしい事はやる必要がなくなります。これらを行う場合にデシベルで計算すると全て加減算計算で済んでしまうのです。誤差はほとんど出ません。これがデシベル計算の最大のメリットなのです。

　さてさて、しかし、数学の世界では乗除算に関してはゼロを入れてはいけない約束事があります。理由は全て答えはゼロになってしまうからです。しかし、現実の世界では弱電回路にゼロを入れても答えは音が無くなるだけです。要するに無音状態になるだけです。何ら問題はありません。そこで私が割り算式のプリアンプを作りました。

　続きは次回です。

　

2020/3/10
　少々、かなり、大分話が道草しました。失礼しました。それではデシベルの計算方法です。

　例えば皆様多く目にする20dBの場合です。この場合先ずは20で割り　d(デシ) 　を消します。すると1Bとなります。これを書き替えますと

　1B=log101

です。これは正確にはロガリズム10を底とする10の一乗と言います。これを正数にするには

　10 　=10

　で10倍となります。これが40dBの場合は10の二乗ですので100倍となります。要するに10の二乗で100です。では30dBでは ?

　d　を外すと　1.5B　となります。これを計算するには

　log101.5 　となります。この計算方法は高校生時代に筆算方法として習いました。しかし、私は残念ながら卒業と共に学校にお返ししてしました。そこで私はコンピューターに計算させております。そのプログラムは

　A=10E1.5

　です。すると　31.62278　算1出されます。しかし、これはデシベル計算のプロク゜ラムをコンピューターへ入れておく必要があります。現在の　コンピューターは残念ながら自ら作ったプログラムはそのまま入れられません。そこでグラフ化しておくと便利なのです。

　

　この自作ソフトの目的は下段の　「デシベル」　と表記された物です。これを使うとあの厄介な対数計算がワンタッチで答えが得られます。今でも非常に便利に使っております。しかし、考えてみると40年もの間何一つ故障もせずに使っている事になります。カシオに感謝です。

　話が少々横道に反れました。

　さてさて、対数表記は算出したデーターをグラフ化する場合に必要不可欠なものなんです。何せ実数でグラフ化した場合に数メーターにも及ぶ物がA4番の方眼紙に収まってしまいます。それも内容により片対数・両対数でほとんど全てグラフ化出来ます。だから我々にとって必要不可欠な物なのです。

　ここで話は少々逆戻りしますが、当時私は対数計算する為に関数電卓を物色しました。しかし、何故か自然対数関数電卓はいっぱいあったのですが何故か常用対数対応の関数電卓はありませんでした。理由は恐らく当時の電卓の設計者は常用対数の必要性に必要性を感じていなかったのだと思います。その結果の当時の関数電卓だったのだと思います。しかし、自然対数も自然現象を数値化かする為に考案された計算方法ですが、電子関係でも結果として自然現象の数値化の為の計算方法です。何故自然現象に対しては自然対数を使うのか　?　私には理解不能です。何せ私は数学者ではありません。更に私は悲しいかな科学者でもありません。私は現実として　「とってもいい加減な存在」　なんです。ここで私から皆様にワンポイントアドバイスです。それは

　　　　　「実質的な勉強をしたければ大学教授の著書は読むな」

　なんです。何せヤツラの著書には結論がありません。単に理論の羅列だけで我々技術やにとって必要な内容がそこにはありません。やはり我々にとっては実業界のお方の著書が有効なのです。何せ実業界の皆様の著書には必ず結論があります。我々には結論が必要なんです。更に私からのワンポイントアドバイスです。それは

　　　　　「師を尊敬するな」　

　なんです。人は師と尊敬する人を崇めてしまったらその師を超える事は出来ません。近付く事はあっても師を越える事は出来ません。よって、恩師は正しい判断かも知れません。しかし、師と崇めてしまうのは間違いです。そのような意味で私には今でも恩師と位置付けているお方がおります。それは私か高校生時代に大々々大嫌いだった古文・漢文の教師です。残念ながら天に召されてしまいましたので名前を申し上げます。それは山田先生と言いました。その大々々大嫌いだった古文・漢文の授業の間にたった言った一言

　　　　　「人を観たら疑うな、学問を観たら疑え」

　です。

　人は何故か文章になるとそれを信じてしまいます。しかし、一歩曳いて考える事も必要だと思います。やはり人とは弱い者だと私は思います。

　今回は道草どころか迷い道に入り込んでしまいました。次回は常用対数についてです。

　写真は40年も前の私が始めて買ったコンピューターです。当時のPCの大ヒット商品はシャープのMZ-80でした。しかし、MZ-80はディスクトップ型です。しかし、写真のカシオのPC-880はポケット型です。要するにテキストを片手に通勤の電車の中で勉強が出来ます。

　当時は私は千葉営業所勤務でしたので電車は逆方向ですので比較的すいておりました。毎日々々テキストを片手に勉強しました。

　当時の言語の主流はパスカル・コボル・フォートランでした。ベーシックは新参者でした。しかし、今後はベーシックだと思いベーシックで独自のプロクラムソースを作りました。

　ベーシックはフォートランの改造型です。その改造型が現在主流のドスです。

　写真は少々以前の測定器郡ですが種類としたら僅か三種類しかありません。それは三種の神器と言われている物です。僅かそれだけでほとんど全ての内容が手に取って解るのです。更に測定器は近年は非常に安価で手に入ります。昔の1/10程度の値段です。例えばミリバルなどはヒューレットパッカードの物は数十万円が当たり前でした。オシロスコープ(シンクロスコープ)はテクトロニクスは数百万円もしたものでした。

　しかし、現在はミリバルは数万円、オシロスコープも数万円で手に入ります。写真の内容の物は昔の物であれば数百万円から一千万円に及ぶと思います。しかし、現在の私の測定器郡は全て足しても数十万円なんです。決して高価な物ではありません。要するに壊れたら買い換えれば事は済みます。良い時代になったものだと思います。

　しかし、多くの人は測定器の使い方が解らないと言います。それは解ろうとしていないからです。私も高校生時代は対数の意味が解りませんでした。しかし、その必要性に迫られると解らない訳には行きません。勉強しました。一生懸命勉強しました。その結果各結果をグラフ化しますと対数の存在意味が痛い程解りました。人は必要に迫られ、更に執拗に直面しますと勉強せざるを得ません。その結果の現在なのだと思います。

　しかし、しかしなんです。対数の実数への計算方法がこれまた難しく、更に面倒なのです。そこで考えました。　「コンピュューターを使ってやろーじゃないの」　

　

2020/3/2
　今回は少々厄介な内容です。それはお約束通りデシベル(ベル)についてです。

　デシベルとは元々の単位はベルである事は前回説明致しました。電圧・電流に関してはベル博士は特例として本来のデシは1/10では無く1/20である事も説明致しました。ベルとは変化量が広範囲に及び正数では表記し切れない場合に使う指数関数です。

　指数関数の場合に対数表記するのですが、対数には自然対数と常用対数の二種類がある事は皆様は高校生時代に習っていると思います。私が習った内容は自然対数とは自然現象に対して使う物で対数の底は2.5だと教わりました。

　それに対して常用対数とは極限られた内容に適用するものでほとんど使わないものだとも習いました。しかし、元々対数表記は広範囲に及ぶ自然現象を正数では表記し切れず、更にグラフ化も不可能な内容に使用する非常に便利な表記方法ですので10を底とする常用対数で何ら問題は無いのでは ?　と、私は思っております。

　この問題は私が思いますに恐らく当時の数学の教師は解っていなかったのでは ?　と、私は思っております。何せ学校の教師なんて者はいい加減な人が多く小学校時代、中学校時代・高校時代は私は各教師から間違った事をいっぱい教えられました。その時は解らなかった事でもその後自分で勉強しますと結果として　「あのヤロー !」　となるのです。しかし、流石に大学時代となると未だ解らない事が非常に多く未だ理解不能の内容がいっぱいありますね。

　その原因は私は大学は工学部の機械科です。機械は私には難し過ぎますので簡単で更に自ら自室で試作実験が出来ますので電子の世界に進んだのです。機械が何故難しいのかと申しますと機械の場合は多くの物が不確定要素の塊なんです。一番の不確定要素は共振問題なんです。これは出来上がってみなければ解りません。機械の最大の不確定要素なのです。

　しかし、電子の場合は全てオームの法則の延長線上に存在します。簡単なんです。問題があるとすれば発振だけなんです。電子回路の発振とは人の身体に例えますと炎症みたいな物なのです。人の場合はその時に多くの場合に抗生物質を投与します。電子回路の場合はシャント抵抗を入れたり位相調整の為にコンデンサーを抱かせたりします。要するに発振を抑える方法はほぼ確立しています。だから電子は簡単なんです。

　しかし、世の中の多くのお方は　「機械は目に見えるから簡単だ。電子は目に見えないから難しい」　と言います。しかし、機械で目に見える事は極々一部でありほとんどは目に見えません。例えばモーターが回っているのは目に見えます。しかし、回転数まで解りません。更にコンベアーの上の製品の動いている事は見えます。しかし、その速度まで解りません。

　その点電子の場合は簡単な測定器があれば全て目に見えます。